四則演算が定義され, 交換法則と結合法則, 分配法則を満たす数の集合を「体」(field)と呼ぶ例えば, 有理数全体 $\mathbb Q$ は通常の四則演算に関して体を成す2の平方根は、後述するように無理数である。2 の平方根は、人類の歴史において極めて初期の段階で発見されており、おそらく最初に知られた無理数であると考えられている。幾何学的には、1辺の長さが 1 の正方形の対角線の長さに相当する。平方根の公式 平方根を含んだ式を計算するためには、次の計算法則を覚えておく必要があります。 a>0、b>0、k>0のとき 実際にこれらの公式が成り立つか、それぞれ証明をしていきます。 証明 √a√b=√ab 左辺を2乗します。 左辺
2
平方根 の 性質
平方根 の 性質-一つの記事にまとめると長くなってしまうので、準備と計算で分けた。 ということで、今回は平方根の計算のための準備をしていこう。 前回 平方根の基礎(基) 今回 平方根の計算(基) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算0 の平方根は 0 のみであり、平方根が一意に定まるのはこのときに限られる。 単位長と任意の長さ a が与えられたとき、 a の正の平方根の長さは定規とコンパスを用いて作図することができる。 定義 数 a に対して、 x 2 = a を満たす x を a の平方根という。



100 数学 平方根 問題 無料の印刷可能なイラスト素材
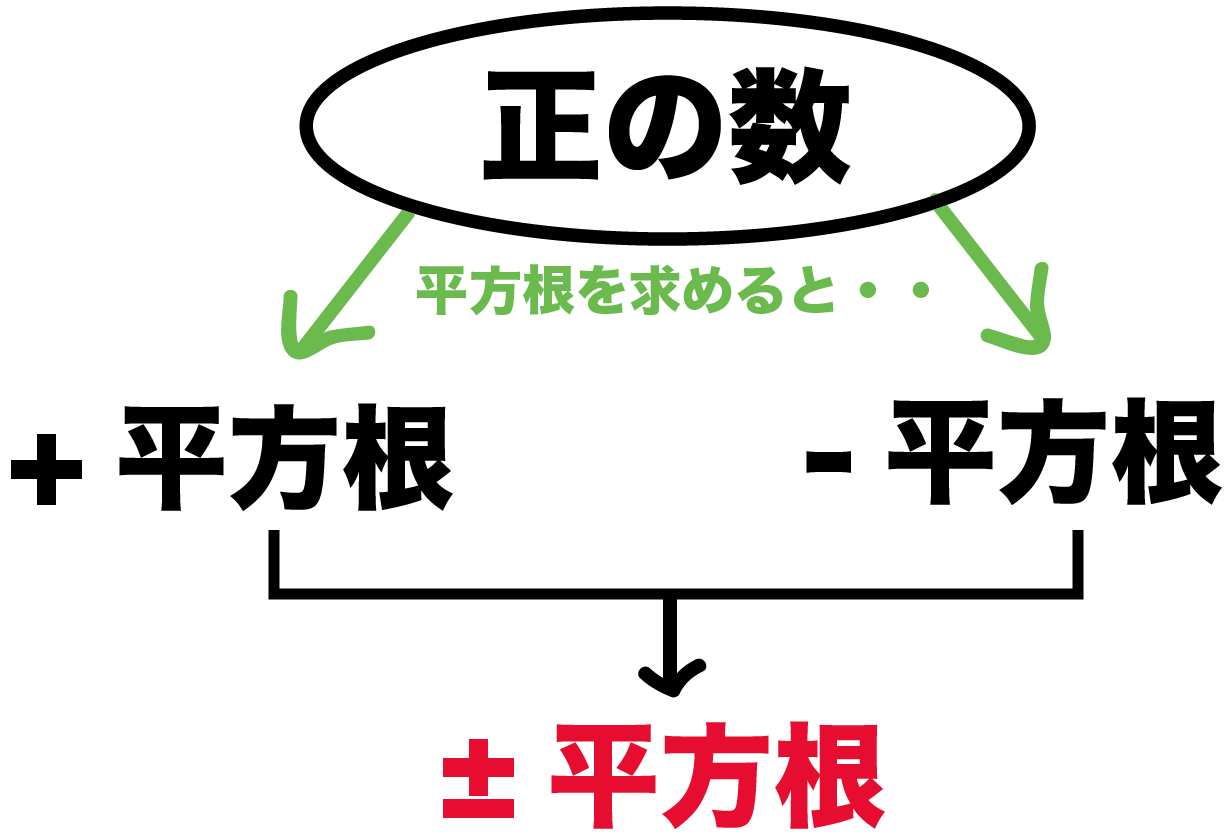
平方根にはどんな性質があるのか?? をみていこう! 性質までおさえればこっちのもんさ。 おさえておきたい平方根の2つの性質 平方根の性質には2つあるよ。 ある正の数の平方根は、 プラスとマイナスのものがある;一つの記事にまとめると長くなってしまうので、準備と計算で分けた。 ということで、今回は平方根の計算のための準備をしていこう。 前回 平方根の基礎(基) 今回 平方根の計算(基) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。
平方根 の意味 √(根号 )の意味 平方根の大小 二次方程式 とその解の意味 関数 の意味 y=aχ 2 の意味 二次関数のグラフの性質→放物線の性質 変化の割合の意味 拡大・縮小の意味 相似 の意味と性質 相似比 の意味と性質 相似条件 の意味 三平方の2の平方根は、後述するように無理数である。2 の平方根は、人類の歴史において極めて初期の段階で発見されており、おそらく最初に知られた無理数であると考えられている。幾何学的には、1辺の長さが 1 の正方形の対角線の長さに相当する。平方根にはどんな性質があるのか?? をみていこう! 性質までおさえればこっちのもんさ。 おさえておきたい平方根の2つの性質 平方根の性質には2つあるよ。 ある正の数の平方根は、 プラスとマイナスのものがある;
平方根の性質(自然数になる) ・ a 2 =a ・ √の中はできるだけ簡単にする ・ 分母は有理化する 75n が自然数となるような最小の整数nを求めよ。 147 2 n が自然数となるような最小の整数nを求めよ。 (1) 75を素因数分解すると 75= 3×5 2 なので 75n =5 3n 3n が自然数になるのは√の中が 自然数の2乗 のとき数の性質大発見(式の利用) 平方根の大きさを比べよう(平方根) 分母を有理化して、無理数の近似値を求めてみよう(平方根) その数を超えない最大の整数を求めよう(数) が分数で表せないことを証明しよう(平方根)数の性質大発見(式の利用) 平方根の大きさを比べよう(平方根) 分母を有理化して、無理数の近似値を求めてみよう(平方根) その数を超えない最大の整数を求めよう(数) が分数で表せないことを証明しよう(平方根)


2


Dainippon Tosho Co Jp Math Files Pdf R3 Sugaku3 Sk Pdf
平方根を小数でかくには 気づかれた方もいると思いますが、平方根を小数で表すことは面倒です。 のようなものは簡単ですが、 などになると小数で書き表すことができません。 もし、 のような小数の値を知りたい場合は二乗をしまくるしかありません。 例えば、平方根の性質 根号を用いて表された数 √ a の加減乗除を考えてみる。a ≥ 0、b ≥ 0 とし、a、b の平方根のう ち負でないものをそれぞれ √ a、 √ b とする1。はじめに √ a と √ b である積の √ a √ b を見ることに する。 ここで(√ a √ b)2 を考える。これは平方根の性質 ( ) 2 = 1 のとき には1,または1が入る。つまり1の平方根は±1 ( ) 2 = 9のとき には3, または3がはいるので、9の平方根は±3



高校数学 平方根の定義と2乗の平方根 A の基本的な扱い 受験の月



高校数学i 3 4 平方根の性質 Youtube
平方根にはどんな性質があるのか?? をみていこう! 性質までおさえればこっちのもんさ。 おさえておきたい平方根の2つの性質 平方根の性質には2つあるよ。 ある正の数の平方根は、 プラスとマイナスのものがある;平方根の性質 平方根は次の性質が成り立ちます。 なにやら面倒くさそうですね。 これを全部覚えますか? 無駄です。 全然覚えなくてOKです。 というのは、 考えれば当たり前のことだからです 。 定義さえ知っていればいいんです。平方根の性質 平方根は次の性質が成り立ちます。 なにやら面倒くさそうですね。 これを全部覚えますか? 無駄です。 全然覚えなくてOKです。 というのは、 考えれば当たり前のことだからです 。 定義さえ知っていればいいんです。



平方根 ルートとは 平方根の求め方を解説 分数や小数の場合はどうやる 数スタ


2
数の平方根に関 心を持ち、近似 値を求めようと している。 分母の有理化を、分 数の性質と、平方根 の定義の2つを用い 導きだすことができ る。 分母の有理 化ができる 分母を有理化すると、その数の近似値を考 えるうえで便利であることを理解してい る。今回から、平方根について学んでいこう 前回 式の計算の利用(難) 次回 計算への準備(基) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算 231 平方根の計算と四則計算・展開・式の値(基)~ 中学3年 数学 ~ Lesson 12 平方根の性質 第2章 平方根 <前:L12 平方根の性質 の問題 L13 平方根の乗法・除法(1)の問題:次> 練習問題1 以下の数にできるだけ小さい自然数をかけて、ある自然数の平方にしたい。



中3数学 平方根の性質 5分で学習 Youtube



平方根 高校数学に関する質問 勉強質問サイト
2 乗すると a になる数のことを a の平方根といいます。このページでは、平方根(ルート)の意味と計算方法、性質、そして大小関係について説明しています。①平方根の性質に興味・関①根号を含む式の計算を文字式の計算①根号を含んだ式の加法、減法、乗①平方根の性質について理解する。 心を持つ。 と対比させて、乗法については交換法法、除法の計算ができる。 ②根号を含んだ式の四則の計算方平方根をすばやく計算するには、数の二乗の表を知る必要があります。 プロパティ 平方根の代数的性質を考えます。 1)積の平方根を抽出するには、各乗数から根を抽出する必要があります。 つまり、それは要因の根の産物として描くことができます。



平方根 中学数学に関する質問 勉強質問サイト



高校数学 平方根と のおさらい 映像授業のtry It トライイット
今回から、平方根について学んでいこう 前回 式の計算の利用(難) 次回 計算への準備(基) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算 231 平方根の計算と四則計算・展開・式の値(基)平方根を計算することは、x 2 =aとなるxの値を求めることになります。 また、中学校では a が0以上の数である場合のみを勉強します。 なぜなら、2乗して負の数になる数は存在しないからです。 ※ 高等学校では、2乗して負になる数も学習します(虚数)今回から、平方根について学んでいこう 前回 式の計算の利用(難) 次回 計算への準備(基) 21 平方根の基本と練習問題(基) 22 計算への準備と平方根の性質(基) 23 平方根の計算 231 平方根の計算と四則計算・展開・式の値(基)


Www City Tatebayashi Gunma Jp Docs Files Suugaku 3 Pdf



キソカク 平方根 中学生 数学のノート Clear
~ 中学3年 数学 ~ Lesson 12 平方根の性質 第2章 平方根 <前:L12 平方根の性質 の問題 L13 平方根の乗法・除法(1)の問題:次> 練習問題1 以下の数にできるだけ小さい自然数をかけて、ある自然数の平方にしたい。平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の平方根を計算することは、x 2 =aとなるxの値を求めることになります。 また、中学校では a が0以上の数である場合のみを勉強します。 なぜなら、2乗して負の数になる数は存在しないからです。 ※ 高等学校では、2乗して負になる数も学習します(虚数)



平方根 4 有理数と無理数 バカでもわかる 中学数学


中3数学12 平方根3 平方根の性質 基本解説プリント 問題 311
2の平方根 性質 2 の平方根(にのへいほうこん、英 square root of two)は、平方して 2 になる実数である。すなわち、表話編歴代数的数代数的整数チェビシェフ分点(英語版)作図可能数コンウェ



5月30日 土 更新動画 復習 乗法公式 因数分解の利用 カレンダー問題 中央義塾



数と式 平方根について 日々是鍛錬 ひびこれたんれん



解の公式の2つの謎 すうがくのいえ
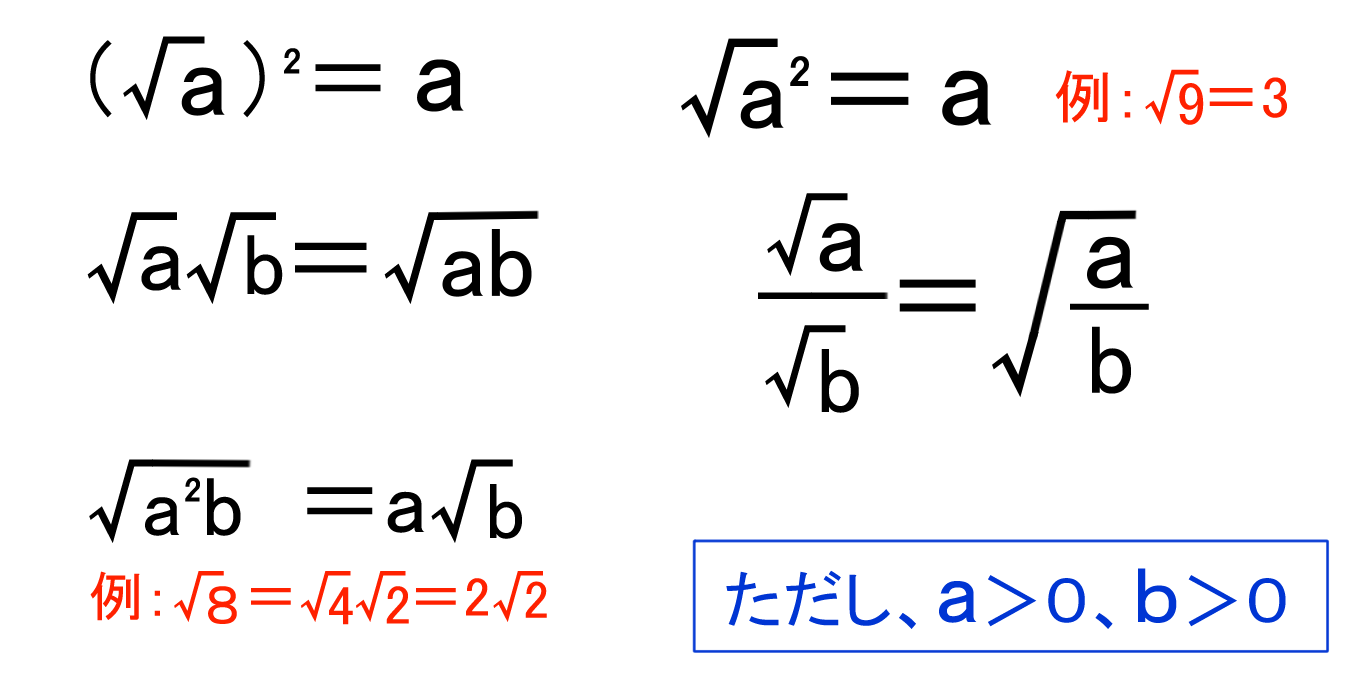


平方根 1 基本のルール バカでもわかる 中学数学


2


Http Chibashikyoken Sakura Ne Jp Sidouann 7 Suugaku Suugaku40 Pdf



無料 中3数学 基本問題 問題プリント 311 平方根3 平方根の性質



平方根 1 基本のルール バカでもわかる 中学数学



平方根の性質 ちょい応用高校数 Youtube


中3数学12 平方根3 平方根の性質 標準問題プリント 問題 311


Http Www Ed2 City Yamato Kanagawa Jp Archive Sugaku 3nen C3 2 Q Pdf



平方根の計算 の中と外を自由に行き来する方法 苦手な数学を簡単に


2



平方根の性質 自然数になる2


Http Www Yatsuo H Tym Ed Jp Pdf Sirabasu H30 3012suugaku1 Pdf


Www Pref Tottori Lg Jp Secure J Suugaku3 3 Pdf


Http Ogose Jh Com 3suugakusidouann Pdf


Www Mext Go Jp Component A Menu Education Micro Detail Icsfiles Afieldfile 16 05 19 3 Pdf


Http Www Nishitokyo Ed Jp J Tanashi1 Shokai 0616 Files 07sugaku Pdf


Www Buzan Hs Nihon U Ac Jp Pdf Syllabus 3suugaku Pdf



歩夢学舎小牧校 平方根の性質とルールを覚えておこう 大小比べる時 2乗したら分かりやすいかも 同じ数字のかけ算の答えも覚えておくといいよね 16 16 256 17 17 2とかね 応時中 小牧中 テスト対策


中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく



平方根 の勉強法のわからないを5分で解決 映像授業のtry It トライイット
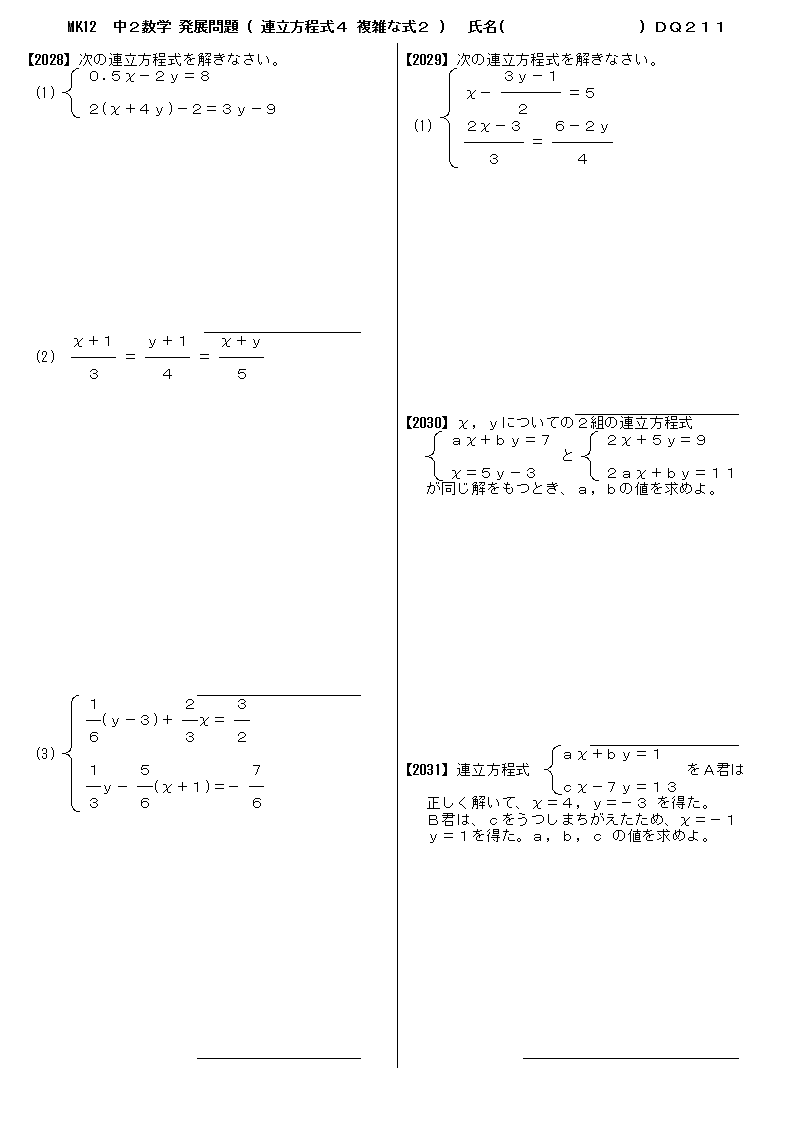


無料 中2数学 応用 発展問題 問題プリント 311 平方根3 平方根の性質



平方根 大小関係を不等号で表す問題を解説 数スタ


2


Http Www Naka H Ibk Ed Jp Action Common Download Main Upload Id 2375



平方根 ルートとは 平方根の求め方を解説 分数や小数の場合はどうやる 数スタ



無料 中3数学 発展 応用問題 問題プリント 311 平方根3 平方根の性質


データ教材 中学数学精選パターンドリル集3年 Usbデータ保存 Gakurin4727 学林舎 通販 Yahoo ショッピング


Http Www Kochinet Ed Jp Susaki L J3 10sugaku Pdf



中学数学 3分でわかる 平方根の性質 Qikeru 学びを楽しくわかりやすく


2



平方根の考えを使った解き方 教遊者



8 2 平方根の性質と計算 イ弋マ本ゼミナール



平方根と平方数 まなびの学園



f数 15 2 平方根 Fukusukeの数学めも



三年数学 平方根 授業ノート 中学生 数学のノート Clear



宇宙を歩く高校数学 基礎



基礎 平方根が苦手な方へ 中3数学 中学生 数学のノート Clear


Www Metro Ed Jp Wakabasogo H Site Zen Content Pdf



数学i 平方根 高校数学に関する質問 勉強質問サイト



負の数の平方根 まなびの学園


2


2



指数 対数の大小判定 基本的性質の利用 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信



この問題の がわかりません 解説お願いします Clear



ワンポイント数学3 根号 ルート の基本と二重根号の外し方


2



高校数学を初めから丁寧に 数学i Vol 021 実数 平方根の性質 Youtube



子供向けぬりえ ユニーク中学 3 年 数学 平方根



例題 平方根の性質 Youtube



2章 平方根 愛知県公立高校入試 数学 単元別過去問 問題プリントと解答 解説



中3数学 平方根 有理数 無理数 平方根 ルート の解き方 教え方 いっしょに勉強しよ



平方根の性質と公式 高校数学 Irohabook



歩夢学舎小牧校 平方根の性質とルールを覚えておこう 大小比べる時 2乗したら分かりやすいかも 同じ数字のかけ算の答えも覚えておくといいよね 16 16 256 17 17 2とかね 応時中 小牧中 テスト対策



中学3年平方根 中学数学に関する質問 勉強質問サイト



100 数学 平方根 問題 無料の印刷可能なイラスト素材



要点 平方根とは Youtube



平方根 2 ルートと平方根の違い バカでもわかる 中学数学



中3数学 平方根の意味 計算のポイントと練習問題 Pikuu



平方根とは 計算方法や求め方 近似値の覚え方 利用問題 受験辞典



中学3年数学平方根 中学数学に関する質問 勉強質問サイト



中3数学 平方根の概念と性質 Youtube



二次方程式の解き方1 チーム エン



100 平方根 の 計算 問題 デザイン文具


Http Www Shinjuku Ed Jp Jh Nishiwaseda cd5184 Pdf


2



f数 15 d 平方根のいろいろな問題 Fukusukeの数学めも



中学数学3年 平方根とその近似値 大小 有理数と無理数 受験の月


2


Http Www Giga Vision Com Wp Content Themes Giga13wp Pdf Curriculum Cm3 Pdf
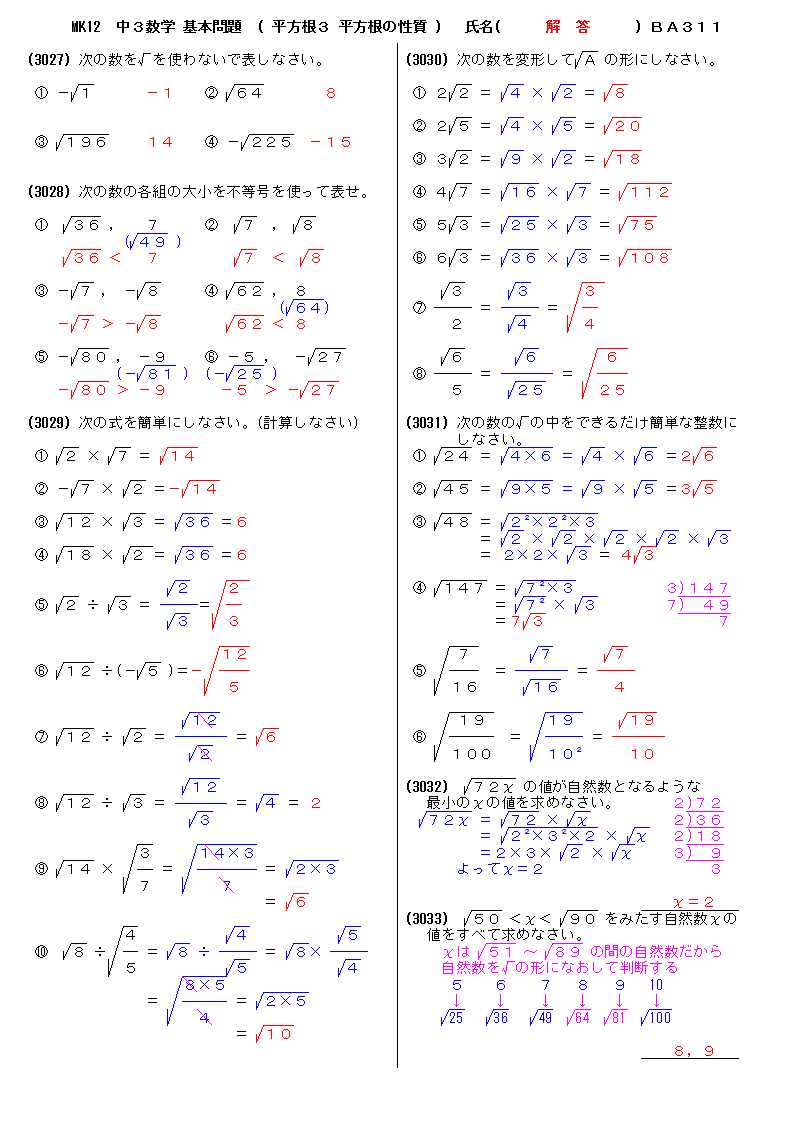


無料 中3数学 基本問題 解答プリント 311 平方根3 平方根の性質



3分で分かる 累乗根とは 定義や計算方法 公式 性質をどこよりも分かりやすく解説 合格サプリ


Www Dainippon Tosho Co Jp Math Files Pdf Guidance Plan H28 Sugaku3 Sk Pdf


2



楽天ブックス わかるをつくる 中学数学 学研プラス 本



二次方程式の解き方 平方根を利用 チーム エン



5の平方根 Wikipedia



2次方程式 1 解き方 因数分解 平方根 平方完成 解の公式 バカでもわかる 中学数学


Www Hokkyodai Ac Jp Files Pdf


中学数学到達度テスト集中3前期 多項式 平方根 2次方程式 2次関数 Gakurin1345 学林舎 通販 Yahoo ショッピング


Http Www E Shiroi Jp Center Sidoan Tyu 3 E5 B9 B4 E6 95 B0 E5 Ad A6 E5 B9 E6 96 B9 E6 A0 B9 Pdf



4 はなぜ1をa 2 3をbとしてみるのではなく 1 3 をaと見る必要が Clear



無料 中3数学 発展 応用問題 解答プリント 311 平方根3 平方根の性質



平方根 A B の形に変形するやり方とは 問題を使って徹底解説 数スタ



0 件のコメント:
コメントを投稿